How to Use

Please select the required calculator and enter either stellar mass or luminosity, hydrogen and metal abundances as mass fractions. Selecting an option from the dropdown below will load the appropriate calculator. Pressing the calculate button will provide the minimum, maximum, and pure-He values for the user input parameters. For more details regarding the structure model grid, see the text description below

Grid parameter range:

1. For mass M, the chemically homogeneous structures (H profile slope of 0) and pure-He structures (H profile slope of inf) have the range 1 ≤ M/Msun ≤ 40, while the structures with H profile slope in between these two extremes have the range 1 ≤ M/Msun ≤ 18.

2. For surface H mass fraction, the range is 0 ≤ X ≤ 0.7

3. For surface metal mass fraction, the values are Z = 0.008 (LMC-like, 0.4Zsun) and Z = 0.004 (SMC-like, 0.2Zsun) where Zsun = 0.02.

Warnings and Errors:

1. Errors are displayed if the inputs are not valid numbers, or if the mass is zero or negative, or if X or Z is negative. X = 0 and Z = 0 are allowed.

2. A set of warnings is printed based on the parameter range of the synthetic model grid. If the inputs fall outside the grid’s tested parameter range, a general warning is shown. If the inputs are significantly beyond the grid range such that the minimum or maximum value of M or L is not truly a minimum or maximum, then a warning is issued indicating that the ML fits may be unreliable. If a calculation fails, especially in the mass calculator, an error is issued.

3. The model grid was computed for Z = 0.008 and Z = 0.004. For any Z value other than 0.008 or 0.004, interpolation or extrapolation is performed, and a corresponding warning is provided.

Python script:

The python script used for this calculator is available here.

Welcome to the Mass-Luminosity Relation (MLR) Calculator page. This web interface enables users to compute minimum, maximum, and pure-helium mass-luminosity relations (MLR), based on the stellar structure models presented in Sabhahit et al. (2025b). This work builds upon existing MLRs in the literature by incorporating structure models featuring a helium (He) core and hydrogen (H) shell - configurations that can result from partial envelope stripping and appear to break simple homology relations.

MLRs in the literature

Typically, based on homology relations \(L \sim \mu^4 M^3\), the minimum luminosity for a given total mass \(M_\mathrm{tot}\) and surface hydrogen mass fraction \(X_\mathrm{H}\) occurs for a fully chemically homogeneous star with \(X(m) = X_\mathrm{H}\). The maximum luminosity occurs for a pure-He model configuration with \(X(m) = 0\), which, from an evolutionary perspective, corresponds to full envelope stripping. Conversely, the maximum mass for a given luminosity and surface \(X_\mathrm{H}\) occurs for a chemically homogeneous star while the minimum mass occurs for a pure-He model. Such maximum and minimum MLRs are provided in Gräfener et al. (2011).

How do we build upon this?

In Sabhahit et al. (2025b), we construct a large grid of stellar structure models in hydrostatic and thermal equilibrium consisting of a pure-He core with an overlying hydrogen shell. The grid is generated by varying four primary parameters: the total mass \(M_\mathrm{tot}\), the surface hydrogen mass fraction \(X_\mathrm{H}\), the metal mass fraction \(Z\), and the H profile slope \(s\) (the definition of slope follows Schootemeijer & Langer 2018) that governs how \(X_\mathrm{H}\) depletes from the surface value to zero at the edge of the pure-He core. The two limiting cases, \(s = 0\) and \(s = \infty\), correspond to the previously known MLRs for fully chemically homogeneous and pure-He configurations, respectively. However, a broad set of new structure models emerges between these two extremes, where the star possesses a relatively massive He-burning core and a low-mass H-burning shell. From an evolutionary perspective, such a structure can result from partial stripping of the envelope via strong single-star wind mass loss or through stable mass transfer beyond the main sequence via Roche lobe overflow.

The inclusion of such He-core + low-mass H-shell structures leads to very interesting MLRs because the H shell can contribute disproportionately to the total luminosity budget. What do we mean by that? See Figure 1, where we show the internal luminosity stratification of a \( 5 \, M_\odot \) model consisting of a \( 4 \, M_\odot \) core and a \( 1 \, M_\odot \) hydrogen envelope. The surface \(X_\mathrm{H}\) is 0.3 and the H profile slope is \(s = 2\). The two spikes in the nuclear energy generation rate mark the two burning regions. The H shell, despite occupying only one-fifth of the total mass, contributes about three-fourths to the total luminosity. This example structure model outputs a total luminosity greater than that of a pure-He model of the same mass, thereby breaking the homology relations.

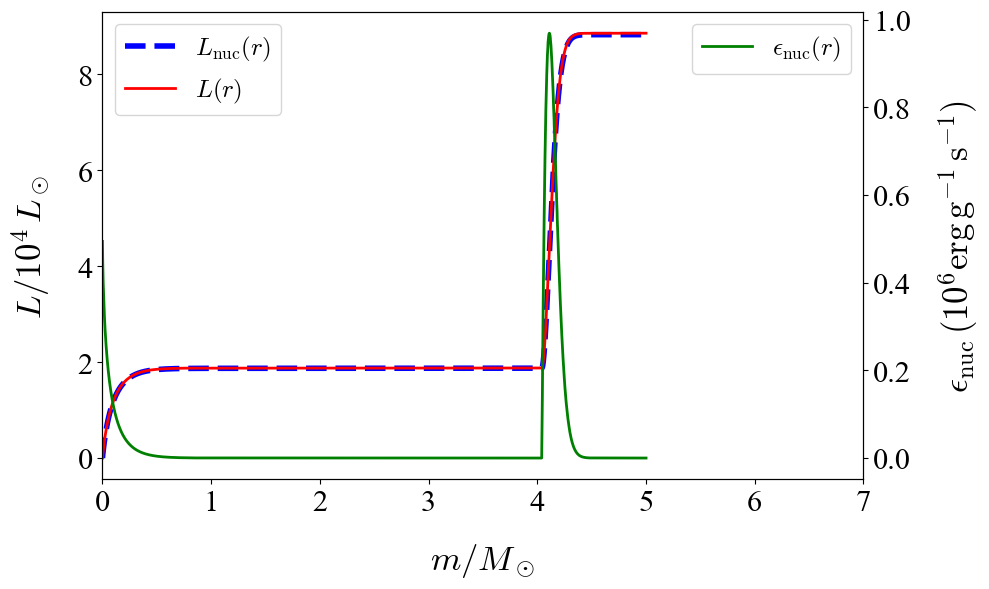
Figure 1

Figure 1: Luminosity stratification of a \( 5 \, M_\odot \) model with a \( 4 \, M_\odot \) He core and \( 1 \, M_\odot \) H shell. The two spikes in the specific nuclear energy generation rate at \(0\) and \( 4 \, M_\odot \) marks the He burning core and the H burning shell.

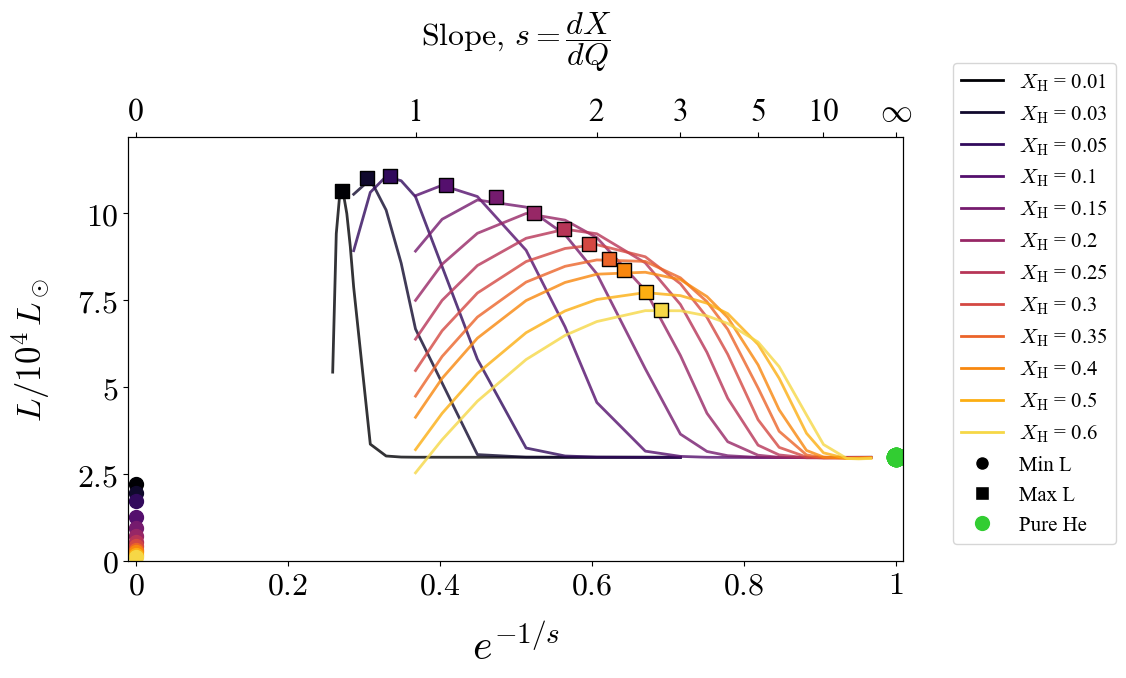
Figure 2

Figure 2: Variation of luminosity as a function of slope \( (0 \leq s \leq \infty) \) for different values of surface \( X_\mathrm{H} \). The total mass \( M_{\text{tot}} \) is fixed at \( 5\, M_{\odot} \). The figure shows the luminosity peak at an \( s \)-value between the extremes \( s = 0 \) and \( s = \infty \).

In Figure 2, we plot the variation of surface luminosity with slope \( s \) for different values of surface \( X_\mathrm{H} \), while fixing \( M_\mathrm{tot} \) to \( 5 \, M_\odot \). We observe that for a given \( M_\mathrm{tot} \) and \( X_\mathrm{H} \), the minimum luminosity still corresponds to the \( s = 0 \) chemically homogeneous model. However, the maximum luminosity does not occur for the \( s = \infty \) pure-He model, but rather at an intermediate slope with a He-core + H-shell structure corresponding to partial stripping. Similarly, the minimum mass does not correspond to the pure-He model either, but again to a He-core + H-shell configuration.

This webpage provides an interactive calculator to predict the minimum, maximum, and pure-He masses and luminosities, including models with such He-core + H-shell structures. Please read the how to use and disclaimers before using the tool. Thank you for reading - enjoy!